💡 Astar 알고리즘이란 ?
각 노드들 사이의 거리를 비교해 더 짧은 길을 찾아 목적지에 최단거리에 도착하는 알고리즘.
1968년도 SRI에서 모바일 자율 행동 로봇 Shakey 프로젝트의 일환으로 고안.
원래는 dijkstra 알고리즘이 1959년에 발표되었지만 astar알고리즘은 이 버전의 확장 버전이라고도 할 수 있다.
💡 Dijkstra 알고리즘
1959년 발표. 그래프의 모든 경로를 탐색하고 최적의 경로 계산.
다이스트 알고리즘은 모든 경로를 알고 그 경로의 거리를 계산해야 하기 떄문에 비용이 많이 발생한다. a*알고리즘은 이러한 문제점을 개선한 것.
이러한 a*알고리즘에 샤키프로젝트를 진행한 스탠포드 연구소는 A new heuristic search method라는 제목을 붙였다.
여기서 휴리스틱이란 경험적 지식을 활용해 답을 구하는 방법을 말한다.
이런 a*는 게임뿐만 아니라 내비게이션, 자연어 파싱등등에도 쓰인다.
💡 a* 알고리즘의 수식
f(n) = g(n) + h(n)
최종 값 경로 값 휴리스틱 예측값
다이스트 알고리즘은 f(n) = g(n)이 다였지만 여기서 h(n)을 더한거라고 생각하면 된다.
휴리스틱 값을 구하는 방법은 일반적으로 해당노드에서 목적지까지의 최단 경로를 사용하지만 상황에 따라 다른 값을 넣어도 무방하다. 그러한 특성 덕에 다양한 상황에 대해 유연하게 대처 가능하다 .
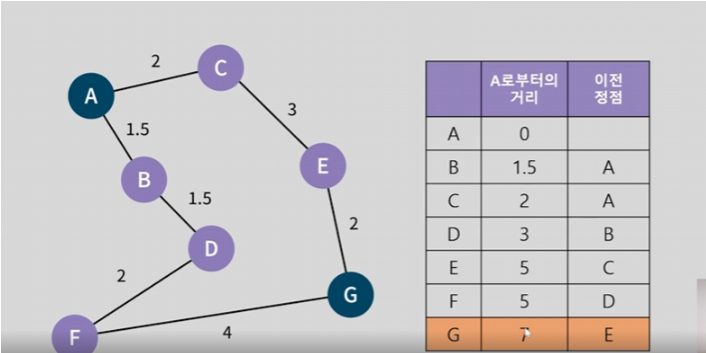
이렇게 구한 최단거리를 각 노드에 저장한다.
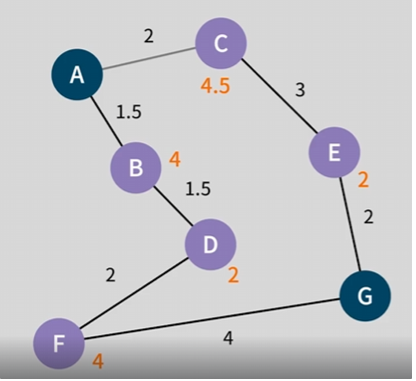
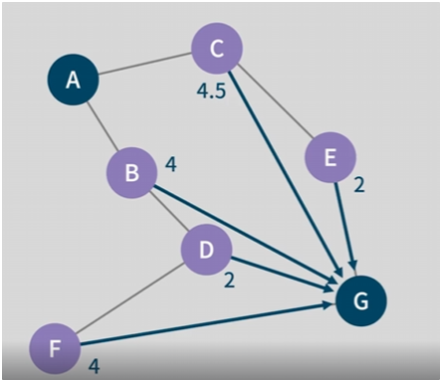
이것을 기반으로 계산 한다면 시작점 A에서 b와 c를 비교했을때 b로 가는 최종값은 5.5 c로 가는 최종값은 6.5가 된다 이렇게 b를 먼저 가게 된다.
여기서 b를 선택했다고 해서 c의 최종값인 6.5가 이후 불필요 한건 아니다 .
이후 탐색은 b에서 진행하되 이후 탐색 값이 c의 최종값인 6.5보다 커질경우 시작점으로 다시 돌아와 길찾기를 실행한다. b로 갔던 경로가 원래 의도인 최단거리를 찾는 것과 멀어질 수도 있기 때문이다.
이런식으로 경로를 찾다 보면 최단 거리를 F - G를 계산 하지 않고 채로 찾을 수 있다 .
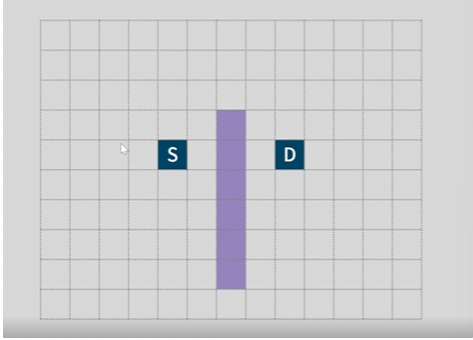
좀 더 실용적으로 보자면 격자(grid) 맵에서의 최단 경로를 탐색해 볼 수 있다.
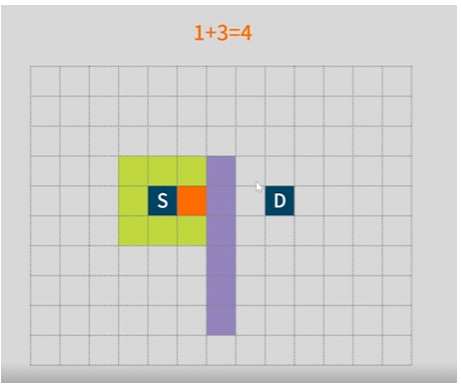
각 노드 사이 거리를 1이라고 치면 제일 처음 경로에서 가장 효율적인 노드는 오른쪽이 되고 이 노드는 출발지에서 1만큼의 거리와 목적지까지 3의 거리 즉 4의 총 거리가 나온다.
그 다음으로 낮은 값도 미리 확인해 보면 대각선의 노드가 4보다는 약간 높은 값이 나오게 된다.
대각선의 노드는 2개의 동일한 총 거리값을 가지게 되는데 이런 경우에 우선순위를 정하는 규칙을 세워야 한다.
일단은 아래쪽의 노드를 우선 가보는 규칙을 세워보자
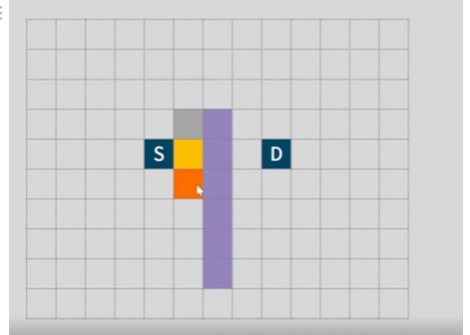
오른쪽으로 먼저 가보니 장애물이 있어서 규칙대로 아래 노드를 다음 노드로 선택해 확장한다.
이때 오른쪽을 고르고 아래쪽으로 가면 2가 되는데 바로 대각선으로 가면 1이 되니 그냥 바로 대각선을 1번째 노드로 선택해 준다.
이 노드가 만약 실패작일때 그 다음 순번은 동점이었지만 규칙에 밀린 윗대각선의 노드가 된다.
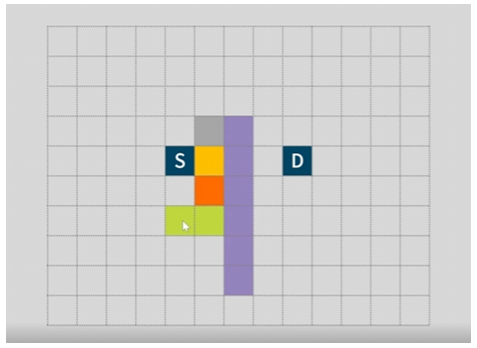
이제 아래로 내려가봤는데 여전히 막혀있음.
다음 노드로 넘어가면 윗대각선 노드의 총계보다 값이 오버되기 때문에 이제 윗대각선을 계산하는데 장애물이 없으니 윗대각선의 윗대각선으로 가게 되고 그것의 아랫대각선 그다음 아랫대각선으로 가게 된다.
여기서 중요한 개념은 노드들의 거리를 계산하고 결정하는데 결정받지 못한 노드의 거리를 버리는게 아니라 어딘가에 저장해뒀다가 나중에 결정 받은 노드에 또 다른 노드까지의 거리가 더해졌을 때 다시 어딘가에 저장해둔 그 노드값을 비교하고 간택 못받은 노드가 더 가깝다 판단되면 다시 처음부터 그 선택 못받았던 노드로 돌아간다.
'TECHIT 멋쟁이사자 강의 정리(유니티)' 카테고리의 다른 글
| [멋쟁이사자처럼 유니티 게임 스쿨 TIL] 5일차 foreach ,group by, linq, list , array 등등 (0) | 2024.06.04 |
|---|---|
| [멋쟁이사자처럼 유니티 게임 스쿨 TIL] 4일차 오브젝트 회전 키 입력 (0) | 2024.06.03 |
| [멋쟁이사자처럼 유니티 게임 스쿨 TIL] 3일차 (0) | 2024.06.01 |
| [멋쟁이사자처럼 유니티 게임 스쿨 TIL] 2일차 C# 클래스 문법까지 (0) | 2024.05.31 |
| [멋쟁이사자처럼 유니티 게임 스쿨 TIL] 강의 1일차 C#네이티브 기초 문법 연습 (0) | 2024.05.29 |
